學生作答線對稱圖形眼動軌跡的分析
作者:師大 宋承彧、林志鴻教授
題目總共有六題,分別為
其中Q1跟Q4與Q2跟Q5與Q3跟Q6的差別只在有紅色混淆(或對稱)線段
受試者要判斷是否為線對稱圖形,並且在作答區勾選是或否
研究目標:
1. 找出學生作答錯誤的原因
2. 混淆線段是否會影響學生對於線對稱圖形的判斷
3. 使用眼動追蹤探討學生觀察線對稱圖形時的認知歷程
分析項目:
1. 作答時長/答案
2. 看題目文字區次數
3. 凝視在紅區的時間長度
4. 看藍區的時間長度
5. 軌跡
接下來分析各題的狀況:
Q1跟Q4:
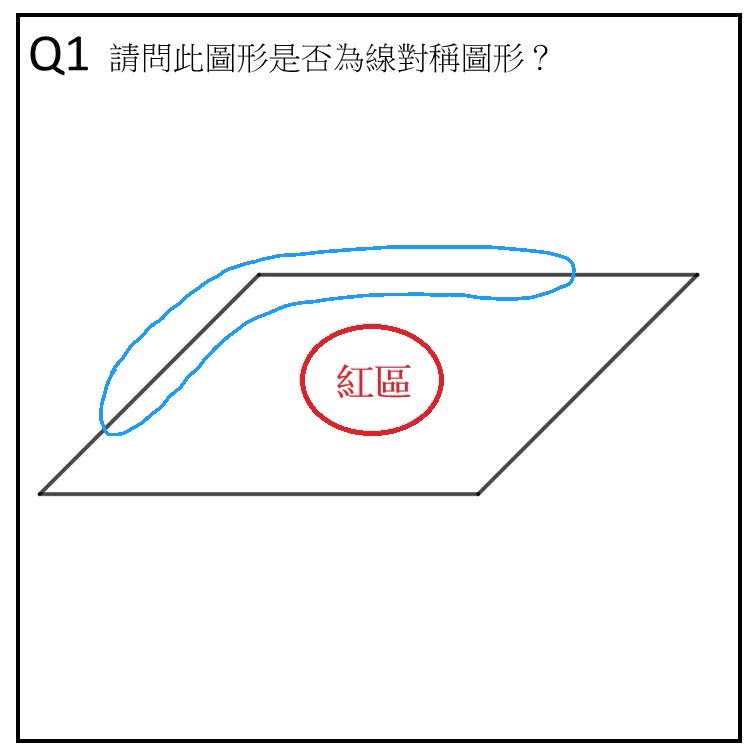
作答時長/答案:27 秒/正確
看題目文字區:1 次
凝視在中心(紅區)的時間長度:5 秒
看圖形邊緣(藍區)的時間長度:4 秒
軌跡:題目→藍區→紅區
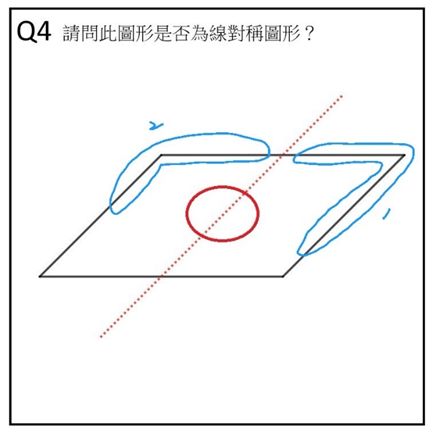
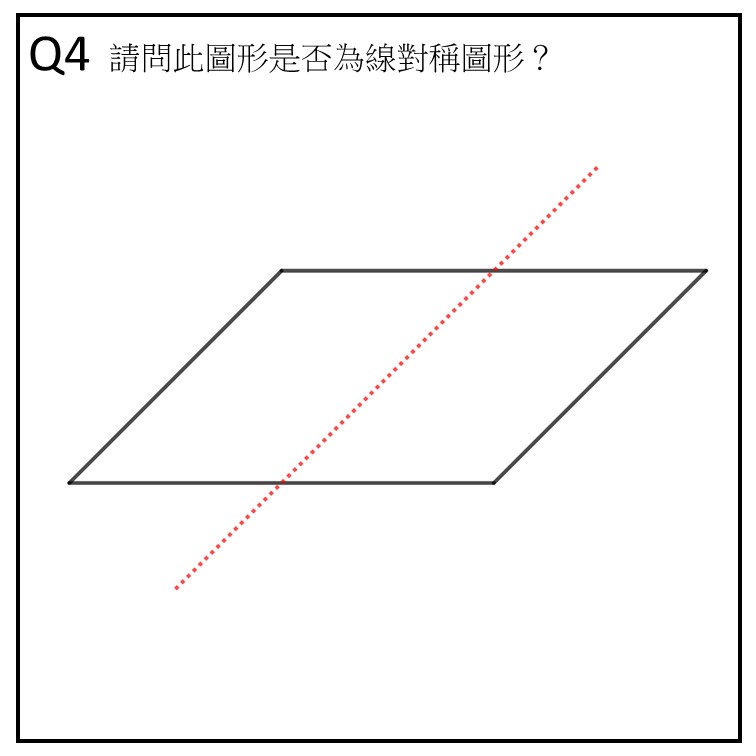
作答時長/答案:23 秒/錯誤
看題目文字區:1 次(但幾乎沒看)
凝視在中心(紅區)的時間長度:6 秒
看圖形邊緣(藍區)的時間長度:12 秒
軌跡:題目→藍區 1(6 秒)→藍區 2(2 秒)→紅區(4.5 秒)→藍區 2(3 秒)→紅區(1.5 秒)→藍區 2(1 秒)
Q1雖然作答時長比較久,但是很多時間都在看空白處,應該是剛進行測試所以在熟悉介面,實際上做的時間大約18秒(以看題目開始計時的話)。再來發現原本做對的題目多了混淆線段後學生就做錯了,在Q4也能發現學生看紅線也看不少時間,所以可以猜想混淆線段具有足夠的誘答力,而且若是以18秒(Q1作答時長)對比23秒(Q4作答時長),可以發現在做這題學生思考時間多了不少,主要是觀察圖形邊緣的時間多了不少。
值得注意的是,學生都沒有看圖形的下方。
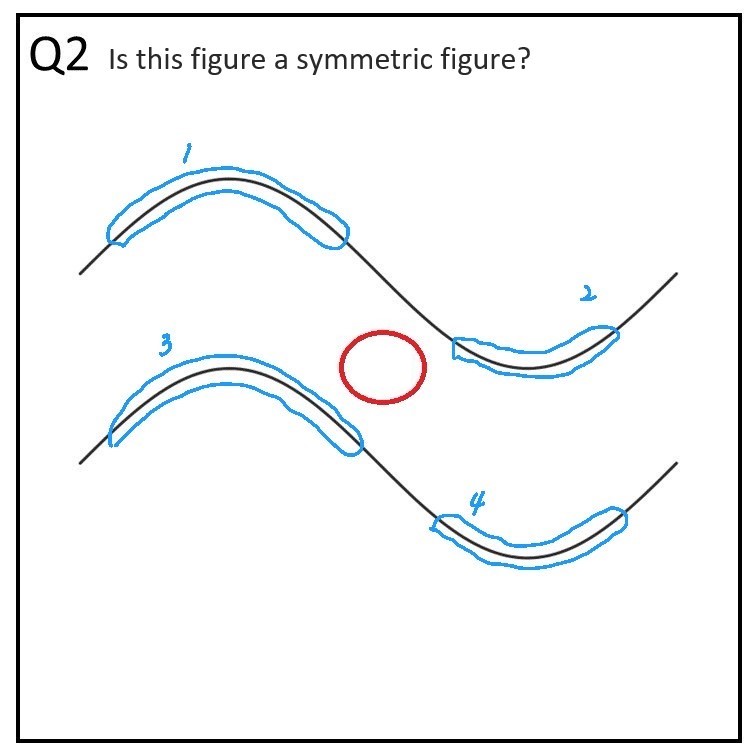
作答時長/答案:25 秒/錯誤
看題目文字區:1 次
凝視在中心(紅區)的時間長度:0.5 秒
看圖形邊緣(藍區)的時間長度:14.5 秒
軌跡:題目→藍區 1(8 秒)→藍區 2(2 秒)→紅區(0.5 秒)→藍區 3(4 秒)→藍區 4(0.5 秒)
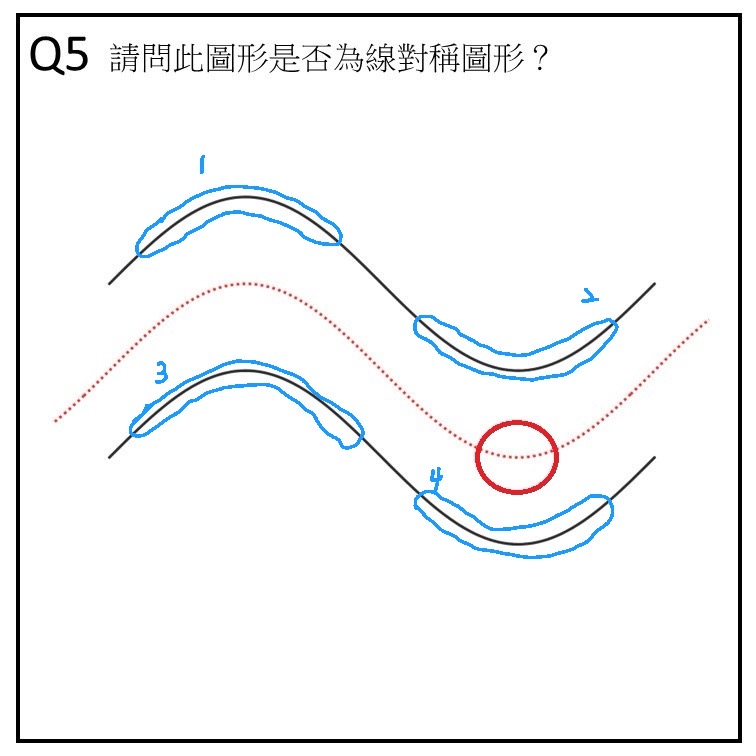
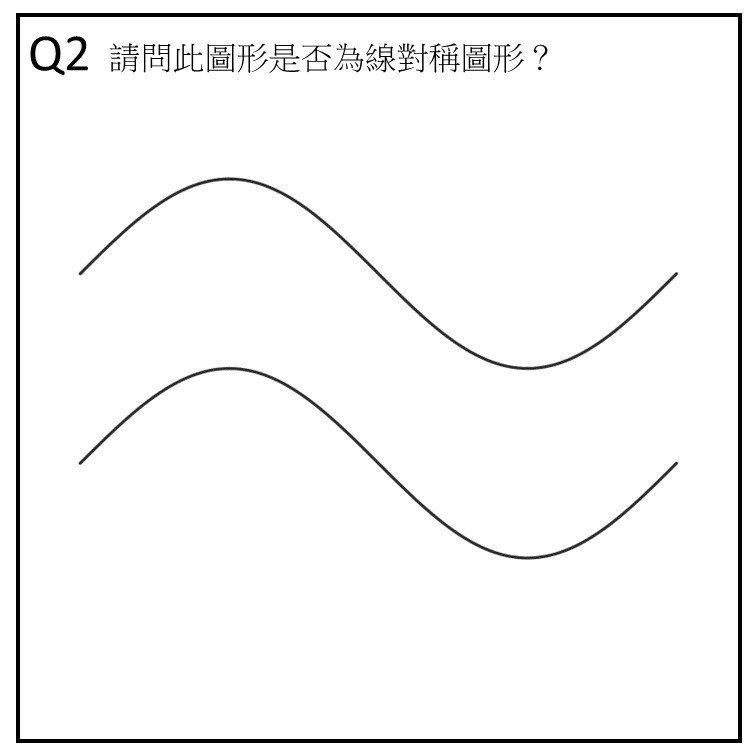
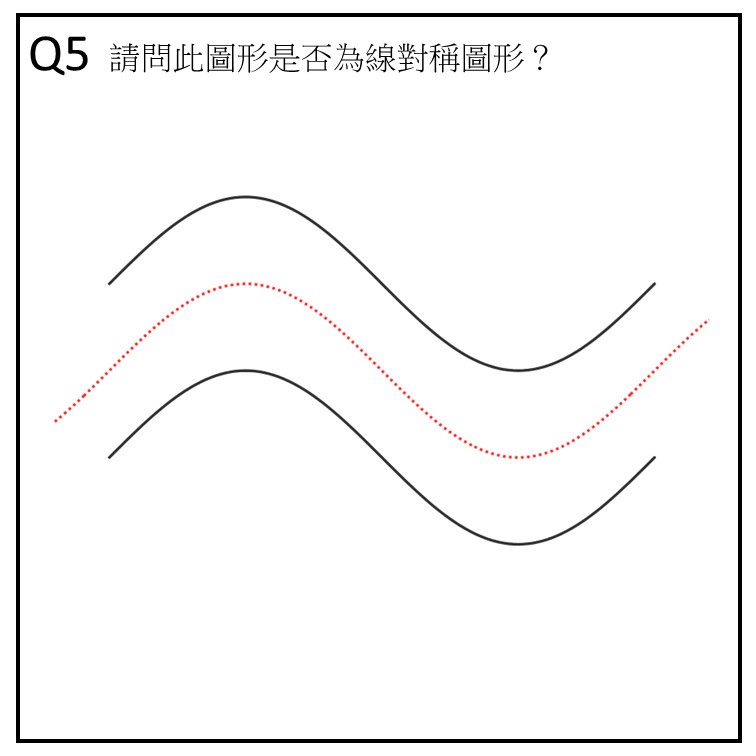
作答時長/答案:18 秒/錯誤
看題目文字區:1 次(但幾乎沒看)
凝視在紅線波谷(紅區)的時間長度:3 秒
看圖形邊緣(藍區)的時間長度:11 秒
軌跡:題目→藍區 2(4 秒)→藍區 1(2 秒)→藍區 3(2 秒)→藍區 2(3 秒)→紅區(3 秒)
Q2 跟 Q5 都做錯,但是 Q2 作答時長多很多,但大多數時間都在看空白處,猜測應該是這種類型圖形學生傾向在腦袋中思考是否為線對稱。至於 Q5 的狀況因為多了混淆紅線,所以學生注意力轉移至紅線(也可以發現注視了紅線波谷三秒),有了可參考的依據讓思考速度快了很多。
值得注意的是 Q2 的藍區 1, 2, 3, 4 都有看,但是在 Q5 中僅看了藍區 1, 2, 3,4 的部分反而沒看。
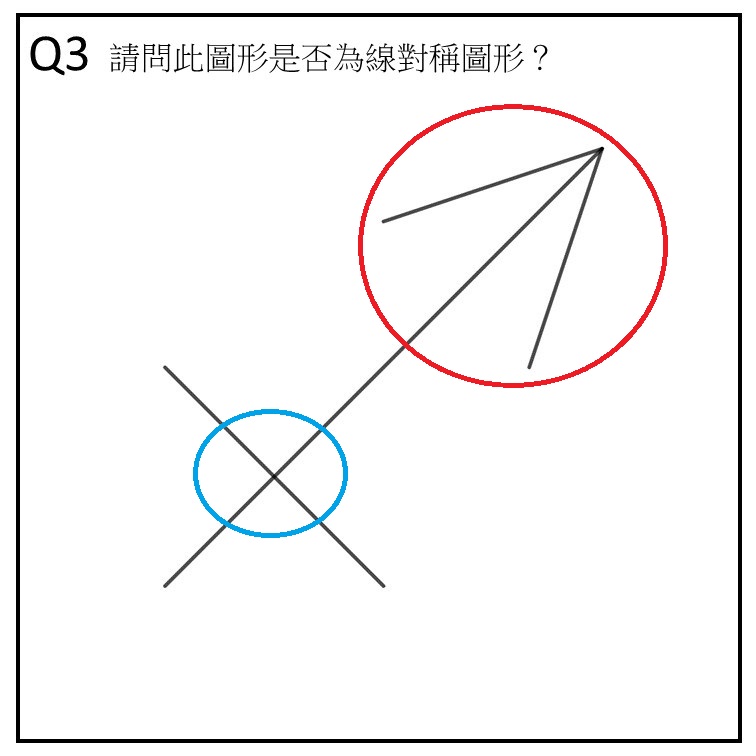
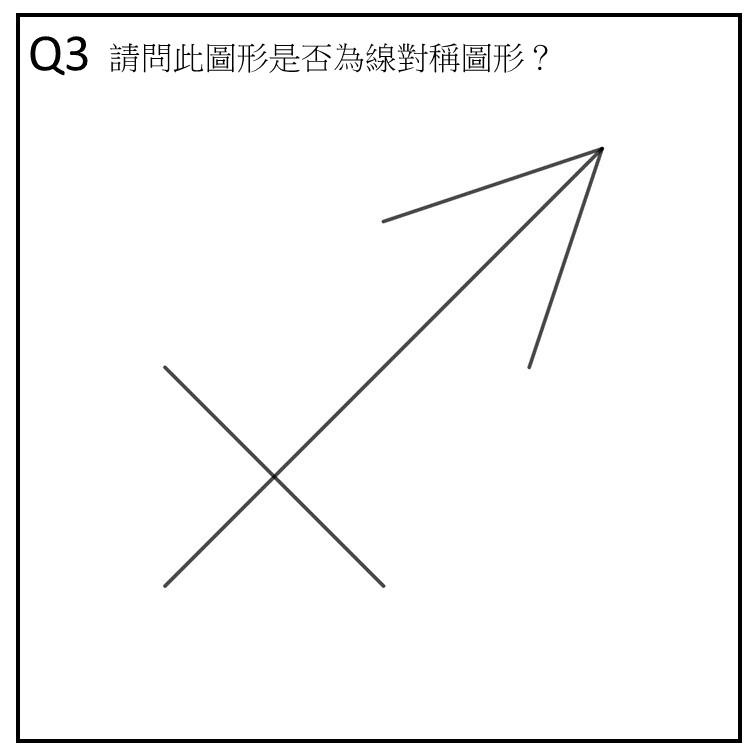
作答時長/答案:14 秒/正確
看題目文字區:1 次(但幾乎沒看)
凝視在尖端(紅區)的時間長度:3 秒
凝視在交叉(藍區)的時間長度:1.5 秒
軌跡:題目→紅區→藍區
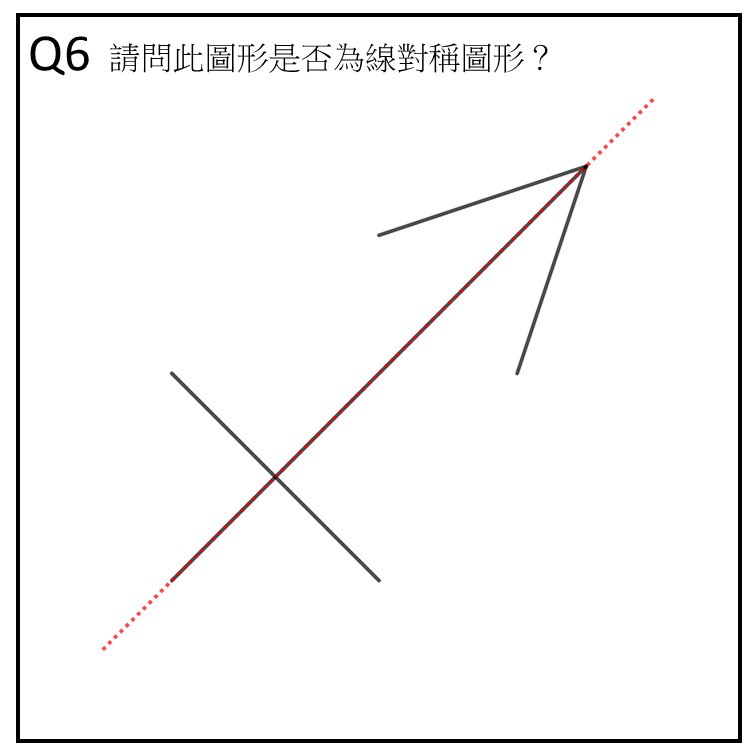
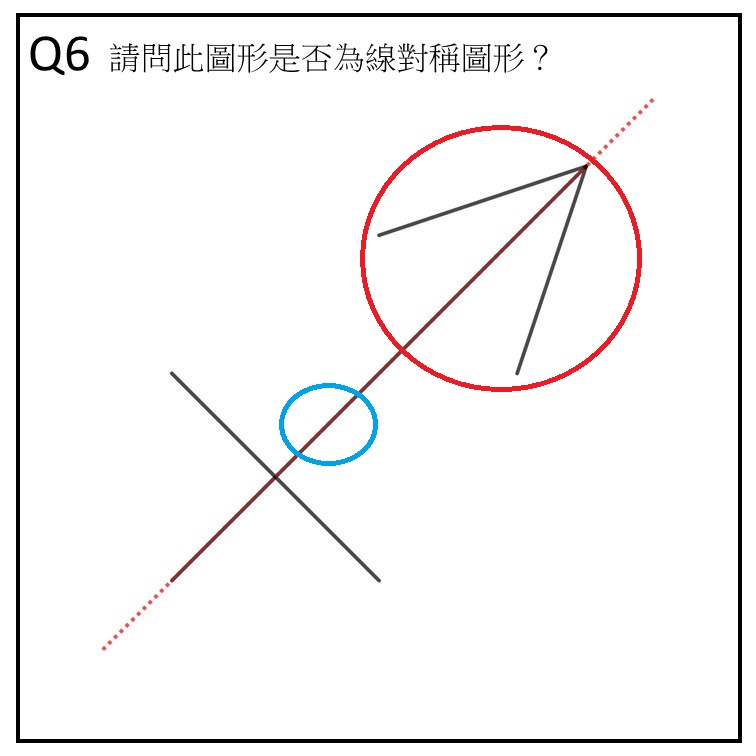
作答時長/答案:7 秒/正確
看題目文字區:1 次(但幾乎沒看)
凝視在尖端(紅區)的時間長度:1.5 秒
凝視在交叉上方(藍區)的時間長度:0.5 秒
軌跡:題目→紅區→藍區
這兩題都正確,其中 Q6 作答時間非常的迅速,可以猜想若是把對稱線給畫上去,可以幫助學生判斷是否為線對稱圖形。兩者的共通點皆是注視尖端(紅區)的時間都是學生看圖形時看最久的。值得注意的是,發現在 Q3 的時候學生會注視交叉(藍區),但是在 Q6 反而是注視交叉上方(藍區),約是圖形的正中央,這部分滿有趣的,可以深入研究。
最後針對 Q1~Q6 全部題目進行分析,可以發現學生閱讀題目時,Q1 閱讀最久,再來 Q2 約在 1~2 秒內,但 Q3~Q6 幾乎只看一眼就迅速看圖形開始判斷,雖然這可能與本研究中每道題都是一樣的問題有關,但仍有不少地方可以討論。
討論:
1. 對於題目文字,可以發現從第三題開始後就幾乎沒什麼看題目,幾乎只有瞥一眼,如果稍微改題目(例如:將線對稱改成點對稱)會發生什麼事情?注視題目的時間突然變意外的長?答題正確率下降?沒注意到變題目,仍然維持前幾題的題目思維作答?
2. 混淆線段/對稱軸具有相當大的誘答力(Q1 答對但 Q4 卻答錯,Q6 做的比 Q3 快很多)對於幾何問題,若是在題目上畫混淆線段,是否會影響學生?若是畫輔助線,是否能幫助學生?線對稱的判斷能力是否與幾何/空間能力成正相關?
3. 學生難以判斷自己是否會線對稱的題目(對題目的難易度均在 5 以下,但答對率為 3/6)
4. 若進行後測不難想像答對率會提高,但對於眼動的分析是否能有不一樣的發現,仍然需要進行更多的探討。
線對稱圖形判別
作者: 海夢